徐  翼 
内江师范学院体育系，四川内江 641112

摘要：本文指出了在运动训练中引入“木桶理论”的若干缺陷，并将体积表达式简化为等价的面积表达式，进而提出了限制运动成绩的“双瓶颈点”概念，以及反映项目对因素板块水平相对需求程度的伸缩系数K值概念，建立了刻画运动素质与运动能力关系的“最大面积”模型，此模型克服了以往仅从单一因素进行量化分析的不足，并具有对各板块位置自动排序的功能，能够较好地从整体角度对运动成绩变化进行动态的综合量化评价，为确定运动训练方向提供决策参考。
关键词：训练方向，木桶理论，最大面积模型，双瓶颈点结构，伸缩系数

１ 引言
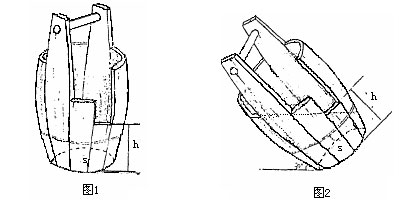
    目前在体育界广为流行的“木桶理论”，来源于日本丰田公司有关企业管理经验。“木桶理论”引入体育界后，使用“水桶模型”(如图1)来形象表述运动素质与运动能力的关系。“水桶模型”形象地将构建木桶的木板比做运动成绩的各决定因素，将木板高度比做运动成绩各决定因素的发展水平，将做木桶的盛水量比作总体运动成绩。“水桶模型”表明，发展水平最低的因素决定着总体运动成绩的高低。延烽教授对此提出异议，认为优异成绩是运动员各方面参差不齐的训练水平动态平衡的结果，“木桶理论”的盲目运用将导致运动训练的盲目性。脱离现实，力图追求各方面训练水平达到同一高度、整齐划一是一种唯心的、不切现实的空想[1]。屈东华、史有宽认为，“木桶理论”的出发点和归宿都是“均衡发展”，“均衡发展”决不等于“平均发展”，同时提出 “木桶合理放置”（斜置）方式（如图2）对决定因素发展水平“均衡发展”的合理性进行了解释[2]。李凯先生用“合金理论”说明与运动成绩的构成，“类似于合金由其各组成单质的特性互相作用、互相制约而共同形成的” [3]。但是，以上理论都仅仅是从观念指出运动素质与运动成绩的关系，未能提供一个能够量化评价它们之间关系的操作办法。正是鉴于这种情况，本文尝试建立“最大面积”模型，对运动素质与运动成绩的关系进行量化分析。

           
2  “木桶理论”的缺陷
2.1  权重值缺失
    “水桶模型”在建立时，将构成“木制水桶”桶帮的木板设定为一样宽（如图1），即设定各成绩决定因素对总体运动成绩的影响权重是相等，这一前提条件显然是错误的。因为不同的成绩决定因素对总体运动成绩的影响权重值肯定不相同。
2.2　最大容积失真
    “水桶模型”中木桶的盛水量极大值，是以木桶处于正立状态为前提的（如图1）。在特定的使用条件下，如果有意识地将木桶向长板方向倾斜（如图2），木桶的储水量肯定比其处于正立时装得多。可见，“木桶理论”计算“水桶模型”容积的前提条件存在严重的局限性，导致其不能正确地反映木桶的最大容积，即不能真实地反映总体运动成绩水平。
2.3　缺少时间限制条件
    发源于企业管理的“木桶理论”，在理论上可以用无限长的时间去弥补某一板块的不足，同时各板块高度提高后就不会再下降。但是，“运动员在达到优异运动成绩前的训练时间是有限的，短暂的运动生涯不可能像企业那样，花上十几、几十年的时间投入精力去完善某一方面，使之达到预想目标”[1]。更为重要的是，随着时间的推移，很多生理方面的因素，其机能水平会自然下降。“木桶理论”在被引入运动训练中时，未能考虑提高板块高度的时间需求与生理机能自然衰老规律两者间的矛盾。“木桶理论”在评估训练效果是时，只计算了某些板块提升造成的影响，却没有将提升这些板块过程所耗时间内，另一些板块高度自然衰减造成的负面影响纳入计算范围，从而导致了对训练效果预期的盲目乐观。

3 “水桶模型”的等价简化表达
    将“水桶模型”容积表达式简化为“面积模型”面积表达式，可以更为简便直观地量化刻画各成绩决定因素与总体运动成绩间的总体关系。展开木桶，将构成木桶的木板依次排列，作一水平直线ＸＹ标出水面高度，四边形XOZY（如图1）的面积就是水桶容积，即总体运动水平。对于图2的“木桶合理放置”（斜置）方式，同样可以简化为“面积模型”面积表达式（如图4）：将构成木桶的木板由高到低排列，作一水平直线ＸＹ标出水面高度，以O点为原点整体旋转板块，使直线XY位置上升，直至四边形XOZY（如图4）的面积达到最大。此时四边形XOZY（如图4）的面积就是木桶合理放置时的水桶容积，即总体运动成绩。

 
4 “最大面积”模型的建立
4.1  “最大面积”模型的因素分析
    有些因素，它对总体运动成绩的影响是单一对应作用，不与其它因素相互关联对运动成绩产生影响，如短跑的起跑反应时，跳高的运动员身高等，它们对运动成绩的影响与其它因素无关。这一类因素称作常量因素，与之对应，互影响制约对运动成绩产生影响的一类因素称作变量因素。常量因素以是单一的、叠加的方式对总体运动成绩产生影响。变量因素是以相互影响、相互制约的方式对总体运动成绩产生影响。“最大面积”模型是讨论的是变量因素与运动成绩间的关系。
4.2  “最大面积”模型的建立
 

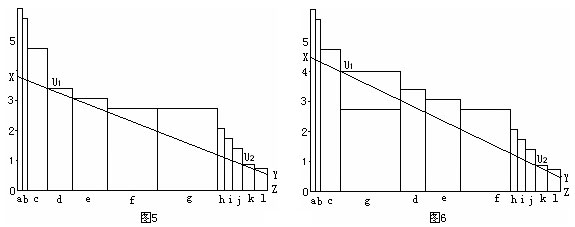
    如果将木桶处于最佳斜置状态，其储水量肯定比其处于正立时装得多。用“最大面积”模型简化最佳倾斜状态下木桶最大容积表述式： 将各变量因素的发展水平作为单一要素板块的高度，将其对总体运动成绩的影响权重值作为单一要素板块的宽度。将各板块由高到低排列，作一条直线ＸＹ，使其位于所有板块内部，并使这条直线下方的四边形XOZY面积达到最大，这个最大面积就是总体运动水平（如图5）。由图5可以发现，在这种特定的斜置状态下，如果将点U1后的一块或几块木板变高，即使这块木板不是最低的一块，容量都可能增大。例如将图5中的g板块高度提升至d板块高度以上，则容量增大（如图6）。
    从图5可以看出，影响最大面积大小的直线ＸＹ由两个点U1和U2决定，这两个点称为瓶颈点。瓶颈点的位置分布只有一种形式：中线的两边各一个。任何一个瓶颈点坐标的变化，都将导致最大面积大小的改变。
5　“最大面积”模型的特点
5.１  权重值的引入
    我们知道，各种变量因素对运动成绩的影响程度是不同的，有的影响极大，有的影响极小。比如说速度力量、绝对力量对短跑项目来说，其影响极大，技术对其影响稍次 ，而战术意识对其影响相对说来要小得多，对运动生物力学、空气动力学之类的理论知识的掌握程度对其影响更小。而对乒乓球项目来说，技术、战术意识对其影响程度相对于速度力量、绝对力量对其的影响程度要大得多。可见，同样一种因素，在不同的运动项目中的权重是不同的；在同一个运动项目中，不同因素的权重也是不同的。
    “木桶理论”错误地将各决定因素对总体运动成绩的影响力设定成相等（如图3）；“最大面积”模型引入了权重值，以各板块因素对应的权重值大小作为其板块宽度（如图5），形象准确地反映了各决定因素对总体运动成绩的影响权重值。
    各种因素与总体运动成绩之间相关程度的单一对应性研究，目前已经有很多文献报道[2][4][5]，其研究结果，可以作为建立“最大面积”模型时，各因素板块权重值的参考数据。
5.２ “均衡发展”思想的直观表述
5.2.1  “木桶理论”对“均衡发展”思想表述的缺陷
    “木桶理论”在表述上，将其中最低水平的决定因素作为决定总体运动成绩的上限（如图1）。按照这一表述，在田径、游泳等体能性项目上，中外运动员在技术、心理素质上都没有显著差异，因而只能推定为是力量、速度、耐力等身体素质的不足限制了中国运动员的运动成绩发挥。推及男女运动员之间的差异，则更应该是如此。那么，在训练上就应该全力发展这些不足，将这几块“木制水桶”桶帮中最低的木板缺口堵住，从而提高运动成绩，而没有必要在这时花大力在技术、心理素质上精雕细刻。但是，在实际训练中，并没有谁放松对技术、心理素质的训练提高，技术、心理素质的训练在很多时候甚至是训练的重点，而这些因素的提高也同样达到了提高总体运动成绩的效果。也就是说，将“木制水桶”桶帮中最高的几块木板再变高，水桶中的水还可以装得更多，这一现象与“水桶模型”理论是相矛盾的。“水桶模型”理论所表达的思想是“等同发展”而非“均衡发展”[2]。
    屈东华、史有宽提出的“木桶合理放置”（斜置）[2]方式（如图2），较好地解释了训练和比赛时的扬长避短、扬长补短现象，从理论上阐明了各种因素合理配置，“均衡发展”的正确性和必要性。但是，“木桶斜置”说由于采用的是立体模型体积表达式，而且没有引入权重值和对板块进行有序排列，因而无法对各因素板块在决定总体运动成绩中的所处的地位和作用做出量化评价。同时，“木桶斜置”说缺少对相对均衡的观念的表述。
5.2.2  相对“均衡发展”思想的正确表述
    “最大面积”模型借助权重值和各板块在四边形XOZY内所占的面积比例，可以清楚地反映各因素板块在决定总体运动成绩大小中所处的地位和作用。由于“最大面积”模型具有自动排序功能，根据“最大面积”模型中各板块高于直线XY位置的程度，可以评价各因素发展的均衡程度。例如在图5模型中，a,b,c三个板块发展程度相对超前，而d,k,l三个板块发展程度则相对滞后。
各板块发展的均衡程度是相对的。受瓶颈点U1和U2的影响，非瓶颈点板块的发展过剩，只表示在“最大面积”以及其它板块水平值一定的前提下，该板块只需要发展到某一水平就够了，高出部分即为浪费。而随着“最大面积”以及其它板块水平值的改变（即直线XY改变），板块的位置可以自动产生排序变化，以前发展程度相对有剩余的板块也可以变为不足。例如g板块发展程度从图5低运动水平中的有余变为图6高运动水平中的不足。“最大面积”模型直观准确地刻画了各因素板块发展的相对均衡程度。
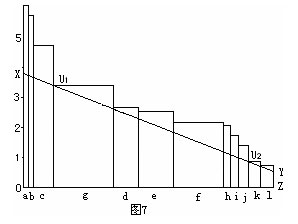
    如图5和图7，两模型中相对应的d,e,f,g四个板块高度均各不相同，但两模型的“最大面积”相等。可见，“最大面积”模型的各因素板块可以有不同的相对均衡组合模式，而“最大面积”值相同，即运动成绩相同。换句话说，条条大路通罗马，达到同样的训练目标，可以有不同的发展道路和模式。这类情况常见于比赛中实力相当，难以分出高下的球队，表现出的风格却迥然不同。
 

5.3  准确反映时效作用
    “木桶理论”未能考虑到运动训练的时效性，它忽视了完善某些低水平因素所需要的时间长度，以及某些因素水平在发展和保持了一定时间长度后必然出现下降的特点。“最大面积”模型不仅可以反映因素水平增大的结果，还可以反映因素水平减小的结果。比如，随着时间的推移，乒乓球运动员技术水平提高和比赛经验更加丰富，相应板块高度增加，而体能水平下降，相应板块高度降低。“最大面积”模型可以将提升技术及丰富比赛经验产生的正面效果和体能水平下降造成的负面影响同时纳入计算范围，准确反映最终结果。
5.3.1  训练投入量的上限性
    很多体能方面的因素，如力量、耐力等，由于体质因素限制，需要恢复和超量恢复，因此一次或一定的时间内所能投入的训练量是有一定限度的。技能方面的因素，受体能和时间的限制，一次或一定的时间内所能投入的训练量同样是有一定限度的。智能因素，特别是比赛经验的获得，由于受赛事安排的制约，在一定时间段内所能够得到的训练更是有限。即使在训练安排上非常科学合理，如在身体恢复期间进行心理、技术、战术、理论等方面的训练，从而使各方面因素的训练投入量得到充分挖掘，但人的时间和精力毕竟是有一定限度的。因此，在训练中各方面的训练投入量不可能无限大地增加。可见，只要有训练的时间限制，就必然有训练投入量的上限。
    训练的目的不同，也会对训练投入量的多少产生制约。比如，作为专业运动员以冲击运动极限作为目标，训练投入量就必须充分的挖掘，使之趋近于个人生理、心理的承受的极限；而把某个运动项目作为业余爱好的训练模式，则只能是在不影响学习工作的前提下来提高自己的运动能力，训练投入量肯定要受到极大限制。
5.3.2  时间对板块高度的影响
    运动训练具有目的性。不管是近期目标还时远期目标，只要是运动训练的目标就必然会带有时间标记。因此，任何训练计划的制定，都必然有具体的训练时间长度条件限制。时间因素对训练效果的影响主要表现在两个方面。第一，在一定的时间长度内，对各类因素的总体训练投入量具有上限。第二，很多生理方面的因素，随着时间的推移，其水平会自然地降低，对这些因素的训练投入，只能够起到延缓其水平降低速度的作用。
5.４  评价板块高度的多重标准性
    不同的项目，对各种素质发展水平的需求标准是不同的。例如，一个体质和智力发展水平属于普通人正常范围值的人，用棋类运动员的需求标准来衡量，其在“最大面积”模型中身体素质板块的发展高度肯定是有余而智力素质板块的发展高度却偏低；如果用短跑运动员的需求标准来衡量，其在“最大面积”模型中肯定是身体素质板块发展高度不足而智力素质板块发展高度有余。可见，处于一个绝对发展水平的某一因素，在不同运动项目中，其相对发展水平是不同的，即反映出来的板块高度不同。显然，采用普通人正常需求标准评价各板块因素所取得的数值，必须要经过某种数学处理，进行修正后，才能作为模型板块的高度使用。这种处理就如同必须将3市尺转化成1米，才能作为物理学的计量长度数据。
    项目对各因素板块相对需求标准与普通人正常需求标准的倍数关系，叫做伸缩系数K。
    K=项目相对需求标准水平值÷普通人正常需求标准水平值
    例如，智能发展水平和速度力量按普通人正常需求标准衡量分别为0.5和1，按短跑项目相对需求标准衡量分别为1和0.4，则短跑项目的智能因素伸缩系数K=1÷0.5=2，速度力量因素伸缩系数K=0.4÷1=0.4。运用数理统计方法，可以找出不同项目各因素板块的K值。采用伸缩系数K值修正后的板块高度，才真实地反映了各因素板块在该项目中的相对发展水平。
    板块高度=伸缩系数K×正常需求标准水平值
    目前各种训练理论对各素质板块的发展水平评估都还是采用的正常需求标准通用计算值，未能考虑到不同项目对各种素质发展水平需求的特殊性，造成了一些相对发展程度已远高于项目需要的素质板块水平值被评估过低，错将长板当成短板。
5.5  训练投入量与运动素质因素水平变化
    相同训练投入量对不同因素以及不同水平阶段上的同一因素的训练效果是不同的。将不同的因素板块提高相同的水平，需要投入的训练量是不一样的。投入相同的训练量，有些因素如力量、速度、耐力等体能类因素，水平越高，提高这类因素水平的训练难度越大，因而提高幅度与其发展水平成反比；而有些因素如战术意识、比赛经验等智能类因素，水平越高，理解能力越强，提高这类因素水平的训练难度越小，因而其提高幅度与其发展水平成正比。
6　“最大面积”模型在运动训练中作用
6.1  “双瓶颈点”在运动训练方向选择过程中的作用
    将某一瓶颈点后的一个或多个板块高度提升至该点高度以上，必然造成最大面积模型图中的板块高度或排列顺序产生改变，使瓶颈点的横坐标或纵坐标值增大，从而造成最大面积增大（如图5、图6、图7）。同样的，如果某一瓶颈点前的某一个或多个因素水平降低至该点高度以下，也必然会造成最大面积模型图中的板块高度或排列顺序产生改变，使瓶颈点的横坐标或纵坐标值减小，从而使最大面积减小。
    在新的模型中，构成瓶颈点的因素可能是原因素，也可能是发展水平低于或高于原因素的另一因素。如将图5中的g板块高度提升至d板块高度以上，则板块的排序发生改变，瓶颈点U1也由d板块变为g板块（如图6）。
6.2  训练投入量与运动训练方向的确定
    将图5中影响权重值较大的g板块和影响权重值较小的l板块分别提升相同的高度，提升g板块可将最大面积增加13.85%（如图6），而提升l板块则只能将最大面积增加3.08%（如图8）。在初级训练阶段，各种因素都较易提高，显然，同样的训练投入量投向对运动成绩影响权重值更大的因素，比将其投向对运动成绩影响权重值更小的因素，所取得的实际效果要好得多（特别是为了在短期内获得明显的效果）。

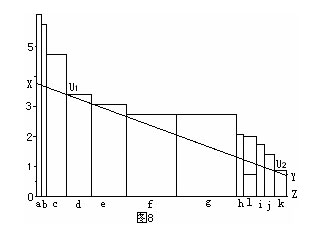
    在高水平训练阶段，某些因素已趋于发展的极限，即使对其训练投入量很大，该因素水平也难以提高，运动成绩提高幅度微乎其微，明显是得不偿失。这时即使该因素是构成木桶的木块中最短的一块，也不可能对其进行很多的训练投入，而是在其它因素上挖掘潜力（这些因素从理论上说是可以无限提高的），这时即使它在构成木桶的木块中是较长的一块，也可以把它变得更长，使总体运动成绩得到一定的提高。这一点从世界优秀选手的心理素质、技术动作、战术意识的等在训练中占有相当大的比重就可以得到验证。如图6反映的是高水平跳高运动员的各方面素质发展水平，g，f，ｅ，ｄ四板块分别代表腿部爆发力、技术、心理素质、比赛经验。在图6中，代表腿部爆发力的g板块已经提高到趋近极限，基本上不可能再有提升的空间。这时，技术ｆ、心理素质ｅ的提升，对比赛成绩的提高，就具有极其重要的意义（如图9）。在图9中，腿部爆发力ｇ、技术ｆ的发展水平均已趋近极限，心理素质ｅ还有一定的提升空间。此时，提升心理素质ｅ、比赛经验ｄ、以及其它一些影响权重值很小但可以提升到点U1高度以上的板块ｈ和ｉ，同样对运动成绩的提高有效（如图10）。在这一提升过程中，即使表腿部爆发力ｇ的水平有一定下降，对运动成绩的提高和保持也不会造成影响（如图９）。

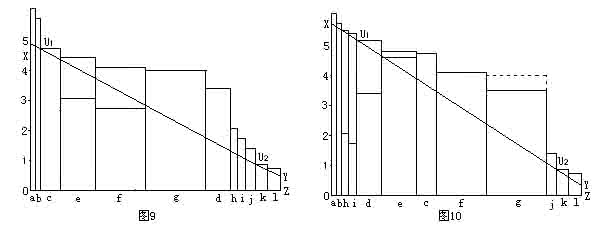
    当然，对于发展程度超出左侧瓶颈点高度的那些因素，由于受其它因素的制约，无论再提高多少，都不会对运动成绩产生影响。比如一个游泳运动员掌握爱因斯坦的相对论对其运动成绩的提高恐怕是没有帮助的。
    教练员常常在无意之中应用“最大面积”原理，根据训练投入量的大小来确定训练方向，而不是根据“木桶理论”原理来选择训练主要方向。比如，参加高考体育术科考试而进行的训练，学生基础差，考试前只有很短的训练时间，而考试中身体素质分值比重又极大（占60%），有的地区甚至只考身体素质（占100%）。这时教练员通常将在“最大面积”模型中权重值宽度比重极大的力量、耐力、速度作为训练的主要方向，在训练中占据了绝对地位，对技术、柔韧、灵敏协调素质的训练几近放弃。训练结果一般都是在几个月内体考成绩突飞猛进，很好地完成了高考目标。至于进了大学后动作不协调，掌握技术较困难，术科学习吃力等后遗症，就不在考前训练的考虑范围了。又如一个高水平田径运动员，已经处于体能衰退的年龄段。这时即使他的技术有不小的缺陷，大部分教练员也不会冒险去改变运动员的技术动作结构。因为在旧有技术动作结构被破坏，新的技术动作结构没有建立起来之前，运动成绩肯定要下降。而经过一定时间段的训练后，新的合理技术动作结构所带来的效益很可能不足以弥补体能素质衰退造成的成绩下降幅度。
6.3  应用“最大面积”模型评价训练方案的步骤
    对训练方案的量化评价，应遵循下列步骤。首先，必须确定达到预定目标所需的时间长度。其次，根据给定的时限，并充分考虑到训练目的、身体恢复快慢、训练时限、场地、气候等诸多因素的影响，建立不同的训练投入量分配方案，正确评估每种方案中各板块因素可能获得的最大训练投入量。第三，确定不同的训练投入量分配方案下各板块因素可能产生的变化，包括时间因素引起的升降变化。第四，根据步骤三得到的各板块高度值，建立显示不同训练投入量分配方案训练效果的“最大面积”模型。第五，将步骤四得到的各“最大面积”模型进行对比分析，优选出最佳方案。

７　结论
    将“水桶模型”等价简化为“面积模型”，可以更为直观地反映各种成绩决定因素对总体运动成绩的影响。传统的“木桶理论”对运动素质与运动能力之关系刻画存在的诸多缺陷，它未能考虑成绩决定因素对总体运动成绩的影响权重值、时间条件对成绩决定因素变化的制约，以及不同项目对各种素质发展水平需求标准的特殊性。“最大面积”模型较好的解决了这些问题，能够更为真实准确地动态刻画运动素质与运动能力间的整体综合关系，反映各因素板块间发展的相对均衡程度，提供不同的发展模式。
    在训练中,受目的、身体恢复快慢、训练时限、场地、气候等诸多因素的影响，对生理和非生理两方面因素的训练投入均是有一定限度的。不同的训练投入量限制，决定了训练投入量分配模式的不同，即运动训练主要方向的不同。采用“双瓶颈点”结构建立的“最大面积”模型，通过建立不同训练投入量分配方案的“最大面积”模型，量化评价各运动素质因素发展水平变化对运动成绩的影响值，进行对比优化，可以为确定运动训练方向提供决策参考。
    对于非生理方面因素与运动成绩之间相关程度的研究，目前尚无具体成果可资借鉴，有待进一步研究。对伸缩系数K值的具体数值研究计算，目前尚未开展。
    本文讨论了“双瓶颈点”结构建立的“最大面积”模型。是否可以建立“三瓶颈点”、“四瓶颈点”等“多瓶颈点”“最大面积”模型，各“瓶颈点”的横坐标取值范围有何要求，都有待于进一步探讨。
此外，对社会发展过程中短期效益与长期效益、掠夺性开发与可持续发展的矛盾，“最大面积”模型也可以给予较为合理的解释。

参考文献
[1] 延烽．对“木桶理论”在高水平运动员训练中不适应性的剖析[J]．北京体育师范学院学报，1999，11（4）：61－64
[2] 屈东华，史有宽．浅谈“木桶理论”在运动训练中的实用性[J]．辽宁体育科技，2002，22（3）：1－2
[3] 李凯．“合金理论”初探[J]．山东体育学院学报，2000，11（1）：1～5
[4]梁景权．摆动腿的摆动对跳远起跳效果的影响[J]．少年体育训2005，（3）：30
[5]米卫国，等．从膝角看不同水平男子跳远运动员摆动腿技术[J]．上海体育科研，2003，24（2）,33