接上期

    作者：孙加可博士
    据此，本人斗胆提出孙氏围棋修正规则如下：
    日本围棋规则必须增添：虚手一次（虚手即为放弃一次下子权），扣除一点，（或称弃权一手，扣除一目）才能成为自恰的体系，才具备与中国围棋规则统一的结构基础。
    如果说日本规则在对局双方手数不相等的情况下，漏洞百出，不堪一击。完全不能自圆其说。应氏规则在某种程度上却能使这种不自洽蒙混过关， 但从根本上来讲，这种蒙混过关是暂时的，在理论上它还是躲不过去的。这其中的道理和蹊跷之处，我们下面详谈。
    如果我们换个方式和角度来提问题：日本规则和应氏规则的根本差异点究竟在何处？难道只是贴目的不同，一个是八目，一个是六目半，只是这一目半的不同？或者还加上应氏规则那种种繁文缛节的共活条例？ 我们能否说：如把日本规则中的贴六目半，改成贴八目，黑胜；再加上那“本草纲目”般的共活条款，日本规则就脱胎换骨了，摇身一变成了应氏规则了？应氏规则长期宣称：此规则和中国数子法完全一致，果真如此吗？在具体的条款上是如何反映出来？日本规则和应氏规则都是以计算双方的空地处的数值来决定胜负的，虽然一个叫目，一个叫点； 一个用人手数，一个用器皿数。难道只凭应氏规则说它跟中国数子法一样，它就一样了？
    应氏规则反复强调，遵循子空皆为地的原则，而真实的情况是，它在这一点上是说一套，做两套。也就是说，没有彻底落实子空皆为地的原则。 道理如下：如果严格执行子空皆为地的原则，那末在对局结束时，应该首先计算双方各在棋盘上有多少活子—— 这是计算“子为的地”。然后，再计算双方各在棋盘上有多少空，就是通常所说的点目——这是计算“空为的地”。加起来为总的占地。然而，实际对局是一人一手棋，双方手数一般是相等的，也就是说“子为的地”一般而言，双方占地相同。所以，大家也就只点目，不点子了。但也有不同的时候，那就是以下两种情况：一种是黑棋收后，黑棋多走一手。另一种是对局的一方或双方有虚手（弃权）存在。如果白棋一方连下五步虚手，黑棋一方步步实手相陪。显而易见，白棋在棋盘上少下了五个白子。这种情况下，“子为的地”双方就不同了。 黑棋“子为的地”比白棋多五子。日本规则只认空，不认子，荒谬之处此刻暂不再说了。但是，以“子空皆为地”为原则的应氏规则，是怎样行使和落实它的原则的呢？
据上所说，应氏规则还是用器皿点目（应氏叫记点），不点盘上的棋子数，如有虚手，并没有专门记下虚手的次数，也就是说，似乎没有把少掉的“子为的地”的数目考虑进去， 加以扣除。那末它是如何解决“子为的地”的计算，是如何履行虚手一次，扣除一点的？应氏规则在对局的前180手中（指一方的手数） 已经自然地具有了“虚手罚点”的效应，但180手后，这种效应就没有了，也就不自洽了。 此话怎解？
    应氏规则规定对局结束，双方要把下过的（被吃的）和没下的尚在棋盒里的己方棋子全放回自己的空中，再计算各自的空（点数）。这个“没下的尚在棋盒里的己方棋子”就是“蹊跷之处”。 有了它，“虚手罚点”的规则已自然发生作用了。比如， 黑白双方各下了100手棋，棋局结束了。    于是， 各自棋盒里应该剩80个未下的棋子。这80颗子填到各自的空中，双方都少了80点，那末双方的空差和没减这80点以前的空差对比是一样的。举例来说：终局时，如黑棋有100点，白棋有90点，黑棋比白棋多10点。如把各自棋盒里剩80个未下的棋子填入各自的空中，黑棋则有20点，白棋有10点。黑棋比白棋还是多10点。——日本数目法就不减这80点。然而，如果黑方此局有三手虚手，白方无虚手，那末黑方实际只下了97手，黑方棋盒里没下的棋子就不再是80子，而是83子了。白方棋盒里还剩80个未下的棋子。这样再依 前述 规则计算，黑棋则有17点，白棋有10点。自然黑方点数就比无虚手时少了三点。 这就是应氏规则在对局的前180手中有“虚手罚点”效应的道理。行文至此，笔者认为，如此把“没下的尚在棋盒里的己方棋子全放回自己的空中”的点空方法，是应氏规则和日本规则根本性差异。这种差异内在的深刻性远高于那种贴目的多少，和为了共活所罗列的“本草纲目”般的条陈。 笔者还认为，这也是应氏宣称的：此规则和中国数子法完全一致的内在理由。它在一定程度上行使了虚手罚点的功能。遗憾的是，这个功能只是在前180手具有，如棋局到此没有结束，后面的手数就没有这种功能。
    补充几点，这也跟虚手罚点有关系。如果说对弈双方手数相等是广义数目法（包括日本和应氏规则）的基础，有人会问，那让子棋该是怎样算呢？比如说让六子棋，黑棋先走六步，手数明显不相等，怎么也可点目呢？应该这样看。比如说让六子棋，按棋界的说法是让一子算半子，让了六子，还三子。108.5子是一半，还三子黑应是183.5子为和棋。 就是说黑184子是黑赢半子，183子是黑输半子。事情如此说，输赢的判定是讲清楚了，让子多少的道理却越讲越糊涂，让六子还三子的并不是任意定下的，这种规定反映了我们老祖宗对子空皆地的深刻理解。让一子的价值是多少？高手们说大概是二十目，那么让六子就是说一百二十目，但是不管让一个子的价值是多少，这个子在棋盘上实际只占了一个交叉点，一个交叉点的位置就是一目棋，让六子就是在棋盘上多放了六个交叉点，一个交叉点的位置就是一目棋，六个交叉点的位置就是六目棋，不管它是由棋子占着或是空着。于是乎，黑方开局先占六个实的交叉点，终局就还给白方空的六个交叉点，就是六目空，三个子。这就是如此明白的表达了子空皆空的原则，也就是还三子的道理。
    国内报上看到的一个例子：一次某城的儿童比赛，两个孩子下到单官，棋局很细。轮到一个孩子下了，他看到没有棋可下了，就说没有了，另一个孩子马上把尚存的很不容易看见的最后一个单官占上去了（就是连下两个单官）反倒反败为胜，这种情况在数子法中是认可的，但在日本围棋规则中是不认可的，原因是同样是虚手不罚所致。
    下面我们举一个简单的例子。在这个例子中，日本规则竟不能判断简单的胜负；而应氏规则在这个例子中和中国数子法大相径庭，两种结果差得离谱。
    这是一个极为简单又颇为好笑的例子, 却生动而明了地展露出此二规则的荒诞之处。可笑之余，也希望引起各位的深思。有两位先生初通围棋，像我一样，是业余中的业余。我们估且称之黑先生, 和白先生. 黑先生持黑棋,白先生持白棋.黑先生只知道两眼活棋，而白先生更次，仅知道虚手在应氏规则中是允许的。于是他俩下了一盘千古难见，又绝不违反规则的棋， 局终时盘面形势如图三

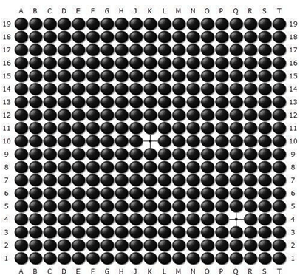
 图三

    对局过程颇为奇特：白先生在全部对弈过程中每一步都用虚手，于是黑先生得以連下359手。由于甲先生只知道两眼活棋，他就在天元处和右下星位各做了一个结结实实一目棋的眼位， 其余全部填满。 经双方同意，对局告终。現先用日本规则判定胜负：黑先生认为：棋盘361个交义奌全属于我。白棋一子沒活， 当然，黑赢。白先生则认为：按照日本规则，黑棋应贴6.5目，现黑棋只有两目，白棋为零目， 理当白棋赢4.5目。请问诸位先生，你们说是谁该赢？双赢？在围棋这个领域，双赢是搞笑的同义词。
    然后再用应氏规则来判断这盘棋的结果。局终，黑先生棋盒里未下的棋子自然为零。黑先生下到180手后还要下—— 棋盘上还有那末多不是禁投点的空处， 你总不能不要他下吧？他不但下完了自己盒中那180粒棋子，还借来了一些下。当黑先生下到359手，棋局结束时双方点数按应氏规则算，到底该是多少呢？黑先生还是两点， 他棋盒里没下的棋子是一个没有，他没有子被吃， 他棋盘上只有两点的空。所以，黑先生的总点数是两点。
    白先生呢？白先生棋盒里未下的棋子是180粒，因为一子未下，全部虚手。棋盘上的点数自然是零点。所以白先生的总点数应该是负一百八十点。黑先生是两点，还要再贴还八点。2— 8—(—180）=174.  总算下来黑先生共赢174点，也就是说黑赢了白八十七个子。换句话说白先生在棋盘上应该还有八十九个活子。然而，白先生在棋盘上是一子未下，一子没有。结论是，应氏规则长期宣称的此规则和中国数子法完全一致的说法并不属实。长期以来子目的换算公式：双方的目差÷2 =双方的子差 并不成立。
    故事还没完。由于双方发生纠纷，又不是正規比赛,棋局又继续下去。黑先生气极一时糊涂，竟在右星位自填一眼，弄得满盘子只有天元一口气。如图四所示：

 图四

    白先生棋力见长。见状手疾眼快，啪的一声，落子天元，顿时把黑压压一遍，360个黑子全部提掉，不证自明,这一手是围棋史上最大的一手提子。于是棋势如图五。
 

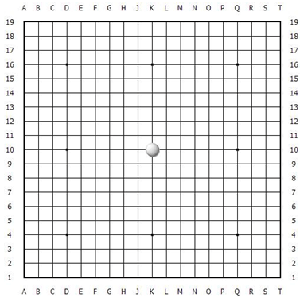
图五

    黑压压乌云一片的满盘黑子刹那间全部消失, 整个光秃秃的棋盘正中天元处挂着一颗白子, 宛如晴空之夜的天极处荧荧生辉的天狼星. 大惊之后的黑先生缓缓定下神来: 情况似乎还不是那么糟,全盘只有一颗白子, 就当重来一盘一样, 只当白棋先走. 大可一战。 黑先生此想乃常情常理, 也符合棋盘上的实际情况. 但可惜的是日本规则的缺陷产生的荒诞这里已经超出了常情常理. 虽然此刻盘上只有一子, 但根据日本规则, 黑先生此刻具有的目数是零目, 而白先生具有的目数是360目. 棋盘上总共才有361个交叉点. 黑棋还得贴6.5目给白棋, 也就是说黑先生在下面的战斗中即使把白先生杀得一子未活, 也还是输.
    黑先生闻之, 此刻的心情真是悲愤难言, 虽然自己的360个子被吃是事实, 对方一子未死也是事实( 因为一子没下!) ,但 自己曾经把棋盘361个交义奌全部据为己有, 曾经使棋盘变化得如同刚刚开局也是事实. 怎么都是自己输? 这是什么规则? 竟荒唐得如此匪夷所思？ 这就是目下的日本规则。这就是当前的日本规则所带来的必然结果.
    日本规则如此，那末应氏规则会得出什么结果呢？让我们来看看。当黑棋自填了一眼，被白棋提了个一子不剩，黑棋的点数自然为零。白棋提了黑棋三百六十子，当然多了三百六十点；前三百五十九手白先生一子未下，故白棋盒里剩有一百八十个棋子，当扣掉一百八十点。再加上黑需贴八点。满打满算，白先生领先黑先生一百八十八点。请各位注意，这就是在图五的情况下，棋局的形势判断。棋盘上虽只有天元处挂着孤零零的一颗白子，满盘空空，但白棋已经领先一百八十八点了，这局棋理论上不能说白一定赢，但黑棋还有法儿下吗？这个例子证明了应氏规则在某些情况下严重失真。
    这里我希望列位不要用：谁也不会下出如此愚蠢的棋，来搪塞，否定问题的存在。我们不是在研究手筋，要点。我们是在研究棋规的合理性。那末，我觉得我们应该有着这样的共识：既然对局双方每一手棋都不违反棋规，对局在双方同意终结后，就应当认可这盘棋，这盘棋也就应该有一个合理的结果，或赢或输或和。
    孙加可博士简介：生物化学研究员，早年留学英国， 生性愚钝，逢事多不解而好问，常不得其就里。自诩深爱中国传统文化，然五经，四书尚未曾读通，毛老三篇倒滚瓜乱熟。少年时抛放于湘鄂川三不管之洪荒地， 首次见到“易经”，不知何物，念成“经易 ”， 复得“千家诗”一本，尚体其美， 手不能罢。后流浪到异域求学，痴迷上围棋和钢琴， 皆不成气候，仅自得其乐，足矣 ！自是学数学出身，崇尚用简单易懂的语言说清混淆不清的事体。愿结天下同好，同乐于华夏文明。
jiakesun@hotmail.com（连载  待续）