徐翼
(内江师范学院体育系,四川内江 641112)
摘 要:运动训练实践中,在确保最大限度提高运动成绩的原则下,根据各因素板块的训练投入产出比实际情况,控制各能力因素板块的发展程度,使各因素板块相互间处于一种“相对均衡”的状态,并使该系统在总体上得到最大程度的利用,可以取得最佳训练效益。“均衡发展”的表现特点为不同的训练道路和模式可以达到相同的训练效果。
关键词:最大面积模型;均衡发展;平衡补偿;非衡补偿
1 相关理论回顾
1.1 “平衡补偿”说
依据日本学者根本勇的“水桶模型”发展而来的“均衡发展理论”认为,竞技能力的整个训练过程中,均衡是相对的,非均衡是绝对的,只有各因素的发展水平不断发展,达到一种新的更高水平的相对动态平衡,总体竞技能力水平才能获得良好的发展和提高[1]。该理论强调,在运动训练中,要加强改善和提高弱势因素水平,使运动员竞技能力构成因素均衡发展,从而达到竞技能力提高的效果,这种补偿方式被称作“平衡补偿”[2]。
1.2 “非衡补偿”说
非衡结构补偿理论认为,在运动员竞技能力形成过程中,虽然竞技能力构成因素没有达到均衡发展,处于非衡结构状态,但由于优势因素的充分发展弥补了弱势因素的不足,使得运动员的整体竞技能力仍能达到相应的水平,这种补偿方式被称作“非衡补偿”[2]。非衡结构补偿理论强调优势因素对弱势因素补偿,总结了“非衡补偿”在运动训练实践中的典型表现:发展运动员特长、形成个人技战术风格。
1.3 “木桶合理放置”(斜置)说
屈东华、史有宽提出的“木桶合理放置”(斜置)[3]方式,较好地解释了训练和比赛时的扬长避短、扬长补短现象,从理论上阐明了各种因素合理配置,“均衡发展”的正确性和必要性。但是,“木桶斜置”说缺少对相对均衡的观念的表述,同时,由于采用的是立体模型体积表达式,而且没有引入权重值和对板块进行有序排列,因而无法对各因素板块的均衡发展程度进行量化评价。
1.4 “最大面积模型”
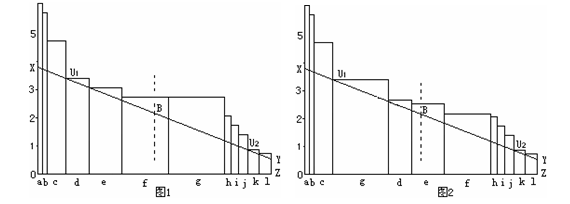
“最大面积模型”以相互影响、相互制约对运动成绩产生影响的变量因素作为模型的构成要素,将各变量因素的发展水平作为单一要素板块的高度,将其对总体运动成绩的影响权重值作为单一要素板块的宽度。将各板块由高到低排列,作一条直线XY,使其位于所有板块内部,并使这条直线下方的四边形XOZY面积达到最大,这个“最大面积”就是总体运动水平(如图1)[4]。
“最大面积模型”显示,影响最大面积大小的直线XY由两个瓶颈点U1和U2决定。任何一个瓶颈点坐标的变化,都可能导致最大面积大小的改变[4]。
2 “平衡补偿”理论对“均衡发展”思想的错误理解
依据日本学者根本勇的“水桶模型”发展而来的“均衡发展理论” ,其基本思想为,发展“弱势因素”通过“平衡补偿”方式,使“弱势”变“优势”,以适应其它因素的发展水平,从而获得新的相对均衡,最终使总体运动竞技能力水平得到全面的发展和提高[1]。显然,“平衡补偿”理论将“均衡发展”错误理解为追求各因素相同发展程度的“等同发展”。
3“非衡补偿”理论的局限
非衡结构补偿理论强调发展优势因素补偿弱势因素达到训练效果,认为 “非衡补偿”与“平衡补偿”是“个别”与“一般”的辨证统一关系,是训练实践中为达到提高运动员竞技能力而采用的两种不同方法[2]。 “非衡补偿”理论的误区在于,未能将发展程度不同的各种因素当着一个“相对均衡”的有机整体系统来对待,未能认识到优势因素与弱势因素间的发展程度是相对均衡而非有余。发展优势因素与提高弱势因素,并不是对另一类因素利用程度不足的补偿,而是为了提升所整体运动水平,在运动训练方向上的不同选择。
4 应用“最大面积模型”正确表述“均衡发展”思想
4.1 平衡点及直线XY斜率的训练学意义
在“最大面积”模型中,以O点为原点,OY为横轴,OX为轴建立直角坐标系,找出线段XY的中点B( , ),我们将点B叫做平衡点。从图?中可以看出,线段OZ长度为一恒定值 ,四边形XOZY的面积= ,平衡点B的横坐标为一恒定值 。显然,四边形XOZY的面积大小取决于平衡点B的纵坐标值大小。训练中采用的一切手段和方法,其最终目的都是通过改变直线XY的状态,提高平衡点B的纵坐标位置,从而增大四边形XOZY面积。
在平衡点B位置不变的前提下,直线XY斜率的变化不会改变四边形XOZY的面积,而是反映出各因素板块间的相对发展水平差距,以及达到相同运动水平,所采用的不同训练思路和发展模式。
4.2 “最大面积模型”揭示的“相对均衡”发展观
在“最大面积”模型中,受瓶颈点U1和U2的影响,非瓶颈点板块的发展过剩,只表示在“最大面积”以及其它板块水平值一定的前提下,该板块只需要发展到某一水平就够了,高出直线XY部分即为浪费。评价各因素发展水平是否合理,也是以各板块水平值一定的一个相对动态稳定系统为前提的。在一个相对动态稳定的系统中,各种因素发展水平殊为不同,却又相互间形成一种较为合理、因素利用率较高的构成关系,叫做“相对均衡”发展。
“最大面积”以及其它板块水平值的改变(即直线XY改变),板块的位置可以自动产生排序变化,以前发展程度相对有剩余的板块也可以变为不足。例如g板块发展程度从图5低运动水平中的有余变为图6高运动水平中的不足。从“最大面积”模型可以看出,增加“最大面积”并非只有提高瓶颈点板块一条途径,发展非瓶颈点板块,改变板块排序位置,同样可以增加“最大面积”。
表示发展程度相对不足的瓶颈点U1和U2板块,其实际发展水平并非绝对落后。瓶颈点只不过是提示我们,在当前这一相对稳定的系统中,如果只能将某一板块提升一定高度,那么选择提升瓶颈点板块,获得的效益最大。但是,这并不意味着提升瓶颈点板块是最佳选择。事实上,在高水平训练阶段,某些因素(特别是生理类因素)已趋于发展的极限,即使对其训练投入量很大,该因素水平也难以提高,运动成绩提高幅度微乎其微,明显是得不偿失。这时即使该因素是板块中较短、较宽的一块,也不可能对其进行很多的训练投入。此时,在其它因素板块上挖掘潜力(这些因素从理论上说是可以无限提高的),即使它是板块中是较长、较窄的一块,把它变得更长,使总体运动成绩得到一定的提高[4],也是一种更为合理的选择。
同理,瓶颈点U1及其以右板块,发展水平都是处于绝对不足状态,只是在当前这一稳定的发展状态中,基于“最大面积”模型自动排序功能,表现为相对有余。如果将这些板块位置前移,一样会呈现出制约“最大面积”提高的不足状态。
显然,任何因素板块都具有发展程度绝对不足与绝对有余的两面性,同时,也具有相对不足与相对有余的两面性。判定任一因素的发展程度,是将其放在其它因素发展程度一定的一个动态稳定系统中,从而得出相对不足、恰当、有余的结论,这一结论与该板块相对于该系统中其它板块发展水平的绝对差距无关。
4.3 板块利用率是评价均衡程度的标准
“最大面积”模型借助权重值和各板块在四边形XOZY内所占的面积比例,可以清楚地反映各因素板块在决定总体运动成绩大小中所处的地位和作用。由于“最大面积”模型具有自动排序功能, “最大面积”模型中各板块高于直线XY位置的程度,直观准确地刻画了各因素板块发展的相对均衡程度。如在图5模型中,a,b,c三个板块发展程度相对超前,而d,g,k,l三个板块发展程度则相对滞后。
事实上,使用“最大面积”模型的总体利用率水平作为评价指标,更能反映各板块发展的总体均衡程度。例如图1的总体利用率为76.4%,图2的总体利用率为79.2%,可见,图2各因素板块发展的相对均衡程度要优于图1。
“平衡补偿”理论采用的“等同发展”方式,提高其它板块的利用率,在高水平运动员的训练实践中,效果并不理想。发展弱势板块,并非提高利用率的最佳途径,改变瓶颈点,通常可以更好的提高其它板块的利用率,使之趋向均衡发展。
在制定训练计划时,要充分计算训练投入量能够产生的训练效益,以实效性和经济性为指导原则,用最小的训练投入量获取最大的训练回报。非衡补偿理论强调优势因素对弱势因素的补偿作用,但在实际操作中,其本质是通过发展优势板块,改变直线XY,增大优势板块的利用面积,从而达到增大最大面积的目的,忽视了训练效益问题。
5“均衡发展”在运动训练实践中的体现
5.1 相对均衡的不同组合模式
如图1和图2,两模型中相对应的d,e,f,g四个板块高度均各不相同,但两模型的“最大面积”相等。可见,“最大面积”模型的各因素板块可以有不同的相对均衡组合模式,而“最大面积”值相同,即运动成绩相同。换句话说,条条大路通罗马,达到同样的训练目标,可以有不同的发展道路和模式。这和“非衡补偿”总结的在运动训练实践中的典型表现:发展运动员特长、形成个人技战术风格是相吻合的。在这些不同的发展模式选择上,充分体现了目的优先、效益优先的原则。
5.2 时效作用对“均衡发展”的影响
在制定长期训练计划时,高运动水平时的均衡发展,往往需要在低运动水平时的非均衡发展,即需要某些板块的提前发展。这种发展方式,可以避免运动水平发展到一定程度时,某一板块不能以相应的速度提高,形成的瓶颈点长期制约其他板块的面积利用率,造成事实上的发展严重不均衡状态,从而严重制约运动水平提高的情况出现,达到最终训练效果的最大化。
参考文献:
[1]郑伟.对“竞技能力均衡发展原则”的探讨分析[J].山东体育学院学报,2005,8(4):95-96
[2]张龙.均衡发展与非衡结构理论在训练实践中的应用[J].太原师范学院学报,2006,3(1):127-130
[3] 屈东华,史有宽.浅谈“木桶理论”在运动训练中的实用性[J].辽宁体育科技,2002,22(3):1-2
[4]徐翼.“最大面积”模型及其训练学意义[J].内江师范学院学报,2008,6(6). |
