孙加可
本文论述了目前数目法围棋规则(包括日本和应氏规则)结构的不合理性。
给出了解决方案,即,增添孙氏围棋修正规则才能成为自恰的体系,才具备与中国围棋规则统一的结构基础。并对日本数目法和应氏规则的根本差异提出了自己的看法。进而推翻了专业围棋界长期以来的以下两个结论:
一.由于中国数子法围棋规则存在打劫收后的情况,其与日本数目法的差异可能为一目。
二.中国数子法围棋规则和应氏围棋规则完全一致。
本文以具体实例证明了中国数子法围棋规则和日本数目法规则的差异可能达七目以上,而并非一目。
同样以具体实例证明了中国数子法围棋规则和应氏规则并非完全一致,存在这样的判例:那就是一盘棋终局时,按照数子法算是黑棋胜,而按照应氏规则判却是白棋胜。
同时对当代棋圣吴清源先生与高川秀格的有争议的一盘棋,给出了与当下棋坛 和出版媒介完全不同的结论。几十年来棋坛和媒介舆论都大势为吴清源先生鸣冤叫屈,吴清源先生本人在自传中也大肆叫屈,认为日本棋院把 吴氏的赢棋判输了。本文用清楚明确的事实,证明了这本不是一“冤假错案”,问题是出在数目法的缺陷上,吴棋圣本是输棋。
其实,数目法的毛病历时久远,, 從歷史的角度縱觀這個問題, 發現了一個有趣的現象, 那就是,智慧和愚蠢, 天才和弱智, 竟是相依而存的難兄難弟: 錙铢必较的智慧豢养了年代久遠的愚蠢, 而搞笑般的弱智却揭示了一種智慧的認知. 人的歷史往往就是這樣。
围棋, 在中华民族五千年文明的历史長河中是一块艳丽夺目的瑰宝, 它并没有因为年代的久远而被蒙上一层层古董般的金黃色的尘沙, 躺在某博物馆或某大学图书馆里, 静待着游人们悠古的观瞻或学者们青灯古塔般的考证, 宛如对那死去的拉丁文字一般. 它的生命力展现在它那永駐的青春,不随岁月的流失而絲毫稍減的魅力上.在这个业已物欲化的纷纷乱乱的忙碌不止的世界上, 仍有偌大的一块园地,一块淨土, 一块圣地. 诚然,外界的杂音不时地透过这淨土的篱笆, 但篱笆里的人们仍無怨無悔地把自己的一生,把自己的爱,自己的事业,自己的智慧奉献给那三百六十一个交叉奌的变幻上. 这些人按普适的标淮, 都有着很高的智商, 他们这种求道般地投入, 棋圣,棋仙,石佛这样的叫法对其中的佼佼者而言也就是颇为贴切的称谓了.
当我们看到围棋这个始源于神州的 “智者之操”, 已经传播于世界各个大洲.当伦敦高雲花园 (Covent Garden)中Go Club里 碧眼高鼻的秃头叼着烟斗在那冥思苦想時,当卷发狮胡的南美人把日本的九段一个个斩得灰头土脸時, 当童音未变的小小孩把挺着将军肚的棋界的腕儿,款儿杀得满脸油汗时, 我们会感叹我们的老祖宗,对世界做出了多大的功德.
由于历史的种种原因, 当今世界上的围棋规则是不统一的, 当前主要有三种,第一种是中国的规则,第二种是日本的规则,第三种是应氏规则。围棋在全球的广泛传播, 使得统一规则成为一个必须面对的事情, 而应氏集团大手笔的投入, 堪称为智力奥运会, 它在举办时间上的选择, 为推广此项智力运动的种种努力, 使得广大棋迷将围棋纳入奥运会的呼声越来越高. 這就更使统一规则成为一件势在必行的大事.那麽, 将各种规则做一番科学,理性的审定也就是必不可少的.说得更通俗明白些, 如果这些规则本身有问题, 那么必须把这些问题先解决了, 才能谈到后面的统一.
这三种规则又可以划分为两大类,第一种数子法规则为第一类,目前主要在中国大陆采用。第二、三种则是数目法规则归其为第二类,目前日本规则主要是在日本、韩国采用,也包括北美,欧洲等地区。因为传统力量的影响,这些地区的围棋爱好者们,也是采用日本规则。至于应氏规则是由应昌期先生发明的,目前主要在应氏杯比赛中采用。数子法的规则很直接,很简单,其法就是在一盘棋结束后,每方将自己的占地计算出来,(即棋盘上空着的交叉点用己方的棋子填满,共活处每方占一半字数,加上棋盘上已活的子数之和即为总占地)谁多谁赢。这里暂不讨论贴子的问题。
数目法规则稍微复杂费解些,其原理是在双方下子手数相等的情况下(终局时,黑方可能会多下一子,我们将在吴老的一盘棋中,详细分析如何处理这种黑棋收后的情况,才为合理),不计算双方下在棋盘上的子数,只是计算各方所围之空的数目。空多一方为胜。这里我们也不讨论先走一方贴多少目为妥。
在举此例之前,我要问当前日本数目法和大陆数子法差异到底有多少? 数子法围棋规则和数目法围棋规则的差异到底在哪里?现在流行的说法是可能差一目棋,就是大陆的数子法,有打劫收后的情况出现,这种情况的存在可使受损的一方因劫材不够,无棋可下,停了一手,眼睜睜地看着受益的一方连走两手,把劫粘上,差掉一目棋。其实,这并不是正确答案。从理论上讲,日本数目法(包括应氏规则)和大陆数子法可能差到五目以上。此话绝非诳语,有例为证:
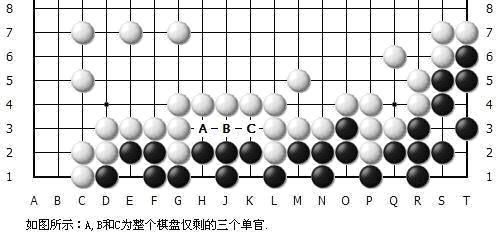
(棋谱) 图 一
如图一所示:A,B 和C 为整个棋盘仅剩的三个单官.还有一条有个单片劫撑着的断头龙.
实际上,这种例子在实战中常常出现。有着中间没眼的断头龙的一方,怕被吃个接不归,早早连接回家,再收其他单官。这已是习惯性的思维方式。实际上,他可得到更大的利益。如果他有足够的劫材,那就是它可以先抢收单官,再打龙头的单片劫,逼得对方无棋可下,自己连走几手。为了使问题的讨论更加简明, 我们假定黑棋有足够的劫材,白棋没有劫材.
具体行棋如图二所示:由黑棋先下.
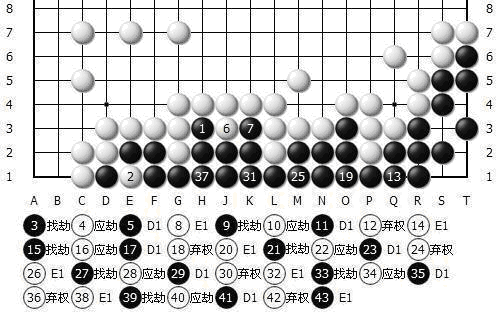
图 二
在日本规则看来,这种走法只是瞎胡闹,只是因在龙头有个单片劫,没被吃个接不归,巳够幸运了. 多走几个单官,少走几个单官对目数的增减沒有任何影响,所以也就沒有任何意义。但在数子法中, 情况就完全不同, 黑多走一步就多占一个子,连着多占七个子,这是多大的差异。 这种情况在理论上的存在仍能说日本规则能和数子规则能统一吗?显而易见, 如果数子法多下七子后的目数与没有多下前的目数一样, 数子法和数目法之间完全丧失了一一对应的关系, 从逻辑上推演, 这种统一已是完全不可能的. 看到此例后,人们还可以把饼做大,就是加多断头处,加多黑方的劫材,使日本数目法和数子法的差异更大。我无意讨论此种差异值的最大可能性,这里我只想说明这种差异值的存在,并给出这种差异出现的原因在哪里。
这个原因就是日本规则中( 某种程度上也包括应氏规则)没有规定虚手一次必罚一点,用常用的围棋语言就是没有规定放弃一手必罚一目。这一点正是关键所在。人们可能要问为什么?请容我缓缓道来,棋界常说:“白(黑)棋什么都沒走到!”这句话的意思是说白(黑)棋既沒占到地.也沒取到势. 并沒有连单官也沒有走到的意思. 但在图一的例子里, 图二的走法给出:白棋从第2手拔劫到第42手无棋可下,弃权, 除了拔拔劫, 只走到一个单官,第6手棋, 其余八个单官全由黑棋走到, 其中包括六个断奌和图一的A,C 两处单官.
首先我要问这多走的七步单官到底值多少目?答案是七目。就是说黑棋多走的七个单官如果换算成目数, 整个黑棋的目数是比未走这七个单官之前多七目,换个方式也可说整个白棋的目数少了七目, 而黑棋目数未变。只有这样祘, 得出的结果才能和数子法结果一致。于是接踵而来的问题是为什么? 因为在整个行棋过程中,我们似乎没见到黑棋目数增长,或白棋目数减少,为什么黑棋要算黑目增加呢?答案就是日本规则必须规定虚手一次,必罚一点才能得到子空皆地的真实的结果。把这种必罚虚手的规定完全反映实际行棋的过程就是,当白棋无棋可下时,则必须往自己或对当空里扔一废子,这样才能得到保持双方行棋手数的相等,这种放一子的结果,就是或己方减少一目,或对方增加一目。这个过程也就是我例子中,凭空增加七目棋的道理。
我在这里所要讨论和强调的是数目法的基础是在对局双方手数相等的情况下人们只需考虑各方所围之空的多少,而落在棋盘上的棋子的多少原则上双方是相等的。如此,就可以自然得出一个合理的结论,倘若没有对局双方手数相等的前提,那么数目法也就丧失了其成立的合理性。假如,一方可以随意不下,导致另一方可连下数手,那么以占地多少为计算胜负的围棋数目法就成为无源之水,无本之木。在以数目法为规则就会出现许多荒诞不经的结果。就是,空多的一方实际占地反而少,空少的一方实际占地可能反而多。众所周知,围棋的规则是以其占地多少为其胜负的判定基准,而地的判定则是子空皆为地,说得更白一点,是一方所活的棋子和其所占领的空地皆为此方的领地。就是子和空的总和为地。这一点在大陆的数子法规则中表现得淋漓精致,不再赘述。然而在数目法中,棋盘上棋子的数目是不计算其个数的,只计算各方所成的空的数目,也就是应氏规则中的点数。那么,在逻辑上就出现上述的可能性:一方成空多但实际占地少,另一方成空少但实际占地多。出现此情况的原因是允许一方不下,进而导致另一方可连下数手。
日本规则包括应氏规则允许虚手成立(虚手即为放弃一次下子权),并不罚点,应该说是这两种规则的致命点,有了这一条,当下的日本规则,(包括应氏规则)则永远不可能和中国数子规则统一起来。此言虽然耸听,但却是铁的事实。因为从理论上讲,有了虚手不罚点就放弃了数目法的前提——双方手数相等。在一方手数下的多,另一方手数下的少的情况下,只看所围空的多少怎么能准确反映占地呢?如果人们进而会问,为什么如此就和数子法永远统一不起来了呢?以上的例子就是一个有力的佐证。
需要注意的是,这种差异在数子法中是不存在的,就是说数子法中无论白棋无棋下时放不放废子在空里,对结果毫无影响,原因是子空皆为地。然而面对数目法的影响是巨大的,原因再重复一遍, 数目法的合理性和前提就是双方下的子的数目相等, 如离开了这个前提, 再谈数目,实在说真无异于痴人说呓语.试想一下, 一方可随意连下八手, 另一方可随意不下, 双方连子数都不一样, 怎么谈空? 又如何反映出子空皆地的结果? 更谈不上能和数子法换算和统一. 我会在后面给出两个简单而又极其明显的例子, 说明某种情况下, 当今的日本规则(包括应氏规则)无法判定简单的胜负.
不说是七目,就是一目的差异在应氏第一届第四局决赛中发生了,应昌期先生也不会含憾而去,未见中国棋手夺冠. 实际上这个问题已经存在多少世纪了.数目法的建立是一件极为智慧的创举:它使棋手双方在行棋过程中能较为容易和清晰地判断彼此的形势优劣. 但随着人们对数目法规则基础的忽略,遗忘,和否定,使对弈中多次出现纠纷, 传说故事中甚至有为了增空,把己方的棋子吞下的故事。 这种纠纷又继尔引发出种种硬牲的规定,结果把规则搞得更为混乱。最著名的例子有以下几个。一、盘角曲四劫尽棋亡的例子,二、带空吃掉一块棋,而不需要把死子棋气都填满提掉的例子,三、棋局结束,到底要不要补棋的问题,著名的例子如吴清源先生与高川秀格先生1959年1月9日 ,10日于热海盐见屋的对局,长期以来,一般舆论认为, 吴清源与高川的那盘棋, 本是高川输了,但在裁判的要求下,要求吴再补一手,于是赢棋反判为输。事情远不是那么简单. 后面我们会详细分析, 其实如果采用不走一手罚一目的规定, 此纷争可轻易解决。这种迷迷糊糊,似是而非已经持续了多少年, 多少代了, 允我一一道来.
会下棋的人都知道,盘角曲四是死棋,因为此棋可有一个劫,但开劫的权力在吃棋的一方,吃棋的一方可先把劫材都补掉再开劫,(这里为使问题简化,我们暂时排除有补不尽的劫材:公活的情况)。被吃的一方因无劫材,干瞪眼只有死掉,这种必然的过程已是定此形为死形的理论依据,但问题出来了,如果吃棋的一方要补十手棋才能吃掉对方,凭什么规定吃棋方不用补呢? 如果人们只把认识停留在硬性规定上,不补棋就是不补棋, 那是完全没有参透这个规定的精髓,其实这个规定是说如果吃棋的一方必须花十手棋,损十目才能吃掉对方这块棋,那么被吃掉的一方也必须陪走十手,损十目的棋; 如果吃棋方必须补上二十手棋, 损二十目空才能吃掉,那么被吃方也必须同时跟着陪上二十手棋,损掉二十目空,来被吃掉. 这才是一个不用补棋的精髓之处,是其数量化的反映。也就是把一个看似强行规定的“蛮横之举” 提升演释为为捍卫数目法基础的合理性,而自然而然给出的结论:只有这样才能使数目法的基础得以成立。显而易见, 不补棋与双方同時对减目数在数量上是等价的。 也就是说日本规则(也包括应氏规则)实际上已导出虚手一步必罚一奌, 而后来又规定虚手可以允许不必挨罚, 这两种前后矛盾的规定就是其不自洽的根本之处。至于第二个例子,带空提掉一块棋,不必把死棋气都填满提掉,也是导致此结论。事实上,从理论上,只要还留在棋盘上的棋都是活棋,只有把它气填满拿离棋盘才叫死。那么被吃的一方就完全有理由叫吃棋的一方把死子提光才承认死,而吃棋的一方为了证实已吃掉对方,只有一步一步紧气吃下去,直到把那已死之棋的气彻底紧光,再从棋盘上提掉。在这不言而喻的共识中,对被吃一方而言,蕴藏着一种公然合理,毫不违反棋规并且堂而皇之的赖皮行为。这种行为由两部分组成。第一步,要求吃棋一方把已死之子全部紧气提掉,否则不承认那是死子 —— 从棋规的理上,这是站得住脚的。第二步,在对方紧气吃时,己方全部虚手以对,一子不下 ——从棋规的理上,这也是站得住脚的,并没犯规。于是被吃一方欢欢喜喜要对方紧气提残子而自己并不下。吃棋一方紧一气则损一目。被吃的一方反得便宜。这种事情想来诸位网上也遇到过。感觉是,苦也!这第二个例子也明确给出为了从规则上防止如此赖皮,也要增加虚手罚点。实际上允许虚手不罚点,或用另一种说法:放弃一手的而无处罚,不仅破坏了数目法的基础,而且违背了围棋竞赛的根本宗旨和围棋的精髓。围棋的进行是在对弈双方的交手中走子得到更大的利益的一方为胜,可如何搞成不走子的一方反得更大的利益?此种结果已经荒唐。(待续) |
